El último mes describí las esculturas matemáticas de Alan St. George, quien a menudo hace uso del bien conocido «número áureo». El catálogo de su exposición en Lisboa menciona a un pariente menos glamuroso, refiriéndose a una serie de artículos en los que «el arquitecto Richard Padovan reveló las glorias del ‘número de plástico’».

El número de plástico tiene poca historia, lo que es extraño considerando sus virtudes como herramienta de diseño, pero su origen en matemáticas es casi tan respetable como el de su primo áureo. No parece ocurrir tan a menudo en la naturaleza, pero, por otro lado, nadie lo ha estado buscando.

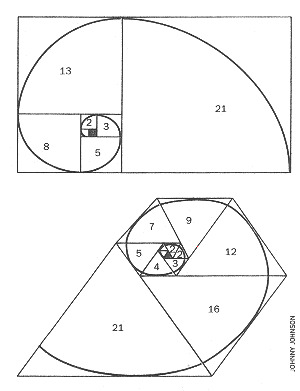
Para poder hacer una comparación, permítanme empezar con el número áureo q = 1 + 1/q = 1.618034, aproximadamente. El número áureo tiene estrechas conexiones con los famosos números de Fibonacci. Esta sucesión puede ser ilustrada por un sistema de cuadrados en espiral (figura 1). El cuadrado inicial en gris, tiene lado 1 lo mismo que su vecino izquierdo. Un cuadrado de lado 2 se añade sobre ambos, seguido por cuadrados de lados 3, 5, 8, 13, 21 etc. Estos números, cada uno de los cuales es la suma de los dos anteriores, forman la sucesión de Fibonacci. La razón de dos números de Fibonacci consecutivos tiende hacia el número áureo. Por ejemplo 21/13 = 1.615384.

Este hecho es una consecuencia de la regla para generar números de Fibonacci: para números grandes, conduce a la ecuación q = 1 + 1/q. Si se añade un cuarto de círculo a cada cuadrado el arco se ajusta a una elegante espiral. Esta espiral es una buena aproximación a la llamada espiral logarítmica que se encuentra a menudo en la naturaleza como en la concha del molusco nautilus. Los giros sucesivos de la espiral crecen a una velocidad aproximadamente igual al número áureo.

Esa es la historia áurea: ahora la plástica. Empezamos con un diagrama similar, pero compuesto por triángulos equiláteros (ver figura 1). El triángulo inicial está coloreado de gris; los triángulos sucesivos se disponen en el sentido de las agujas del reloj. La espiral que se genera es de nuevo aproximadamente logarítmica. Para que las formas encajen los primeros tres triángulos tienen todos lado 1, los dos siguientes lado 2, luego los números van 3, 4, 5, 7, 9, 12, 16, 21 y así. De nuevo hay una regla simple: cada número se obtiene saltando el anterior y sumando los dos anteriores a ese. Permítanme llamar a esta sucesión la sucesión de Padovan en honor de Richard Padovan. (Es curioso que Padova es la forma italianade Padua y Fibonacci era de Pisa que está a unos 160 km de Padua).

De forma algebraica las reglas para generar las series de Fibonacci F_n y de Padovan P_n son como siguen:

F_n + 1 = F_n + F_n − 1, F₀ = F₁ = 1

P_n + 1 = P_n − 1 + P_n − 2, P₀ = P₁ = P₂ = 1

El parecido familiar es muy notable. El número de plástico, que de ahora en adelante llamaré p y cuyo valor aproximado es 1.324718, surge como el límite de números sucesivos de Padovan, igual que el número áureo surge de la sucesión de Fibonacci. La regla de formación conduce a la ecuación p = 1/p + 1/p² o equivalentemente p³ − p − 1 = 0; el número p es la única solución real de esta ecuación.

La sucesión de Padovan aumenta mucho más lentamente que la de Fibonacci, porque p es menor que q. Hay muchos patrones interesantes en la sucesión de Padovan. Por ejemplo la figura muestra que 21 = 16 + 5, porque los triángulos adyacentes que comparten arista tienen que encajar. Por tanto, una regla alternativa para derivar más términos es

P_n + 1 = P_n + P_n − 4

Algunos números como 3, 5 y 21 son a la vez de Fibonacci y de Padovan. ¿Hay más? Si es así ¿cuántos? ¿hay un número finito o infinito de ellos? Algunos números de Padovan como 9, 16 y 49 son cuadrados perfectos. ¿Hay más? Sus raíces cuadradas 3, 4 y 7 también son números de Padovan. ¿Es una coincidencia o una regla general? Estas y otras preguntas merecen un estudio adicional.

Otra forma de generar los números de Padovan es imitar el uso de cuadrados en la sucesión de Fibonacci pero con estructuras cuboides, cajas de caras rectangulares. Así obtenemos una especie de espiral tridimensional de cajas (ver figura 2). Empieza con un cubo de lado 1 y pon otro igual adyacente. El resultado es un cuboide 1 x 1 x 2. En la cara 1 x 2 añade otro 1 x 1 x 2, obteniendo un cuboide 1 x 2 x 2. Luego en la cara 2 x 2, añade un cubo 2 x 2 x 2 para formar en conjunto un cuboide 2 x 2 x 3. A una cara 2 x 3, añade un 2 x 2 x 3 para formar en conjunto un 2 x 3 x 4 y así sucesivamente. Continua añadiendo cuboides siempre en sucesión este, sur, abajo, oeste, norte y arriba. En cada fase el nuevo cuboide que se forma tendrá como lados tres números sucesivos de Padovan.

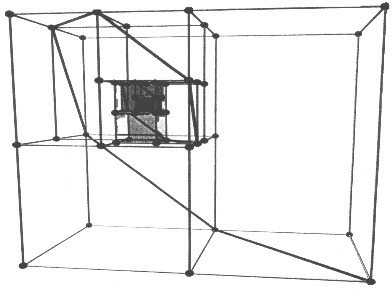
Más aún, si conectas caras sucesivas cuadradas de los cuboides con lineas rectas, tienes una espiral. Resulta incluso que esa espiral yace en un plano. St. George ha basado una escultura en esta construcción, hecha de barras rígidas conectadas por bolas agujereadas en sus esquinas. (¿Qué diagrama hace la intersección de este sistema de cuboides con esta forma plana?)

Una sucesión con la misma regla de formación, pero empezando en distintos valores, fue estudiada en 1876 por el francés Edouard Lucas. En 1899 sus ideas fueron desarrolladas más por R. Perrin, y la sucesión se conoce ahora como sucesión de Perrin A_n. Los números de Perrin se diferencian de los de Padovan en que A₀ = 3, A₁ = 0 y A₂ = 2. De nuevo la razón entre términos consecutivos de Perrin tiende a p, pero Lucas se dio cuenta de una propiedad más sutil. Siempre que n es un número primo, divide exactamente a A_n. Por ejemplo 19 es primo, A₁₉ = 209 y 209/19 = 11.

Este teorema proporciona una curiosa forma de comprobar que un número es compuesto, es decir no primo. Por ejemplo cuando n = 18, tenemos que A₁₈ = 158 y 158/18 = 8.777 que no es un número entero. Por tanto, 18 debe ser un número compuesto. Podemos usar por tanto los números de Perrin para comprobar la no primalidad: cualquier número n que no divida a A_n es compuesto.

Si n divide a A_n, ¿debe ser n necesariamente primo? Eso no se sigue del teorema de Lucas más que «si llueve entonces me mojo» implica que «si me mojo entonces llueve». (Puedo haber caído en un charco un día perfectamente seco). Aún así es una cuestión fascinante. Nadie ha encontrado un número compuesto n que divida a A_n, pero nadie ha demostrado que esos números conocidos como pseudoprimos de Perrin no existan. En 1991 Steven Arno del Supercomputing Research Center en Bowie, Maryland demostró que los pseudoprimos de Perrin si existen tienen al menos 15 dígitos. Estaría encantado de oír progresos recientes.

La conjetura de que no existen pseudoprimos de Perrin es importante, porque el resto de dividir A_n entre n puede calcularse muy rápidamente. Si la conjetura es cierta, este resto será cero sí y solo sí n es primo, por tanto proporcionando un test rápido de primalidad. (De hecho en 1982 William W. Adams de la universidad Daniel Shanks de Maryland encontró una forma de calcular este resto en log n pasos.) Por tanto, la conjetura sería aplicaciones útiles para los códigos secretos, que hoy en día dependen de las propiedades de los grandes primos. Al igual que su reluciente primo dorado, el plebeyo número de plástico genera ricas espirales de ideas.

Referencia

archive.org